链表

本篇为个人笔记，内容或有错误。
图片部分源于代码随想录，侵删。

链表

链表是一种通过指针串联在一起的线性结构，每一个节点由两部分组成，一个是数据域一个是指针域（存放指向下一个节点的指针），最后一个节点的指针域指向null（空指针的意思）。

  1. 链接的入口节点称为链表的头结点也就是head。

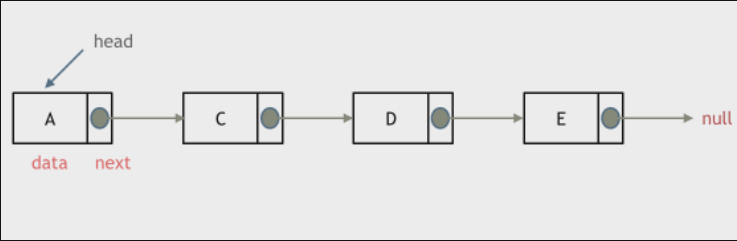    20220526212803
    20220526212803

  2. 双链表：

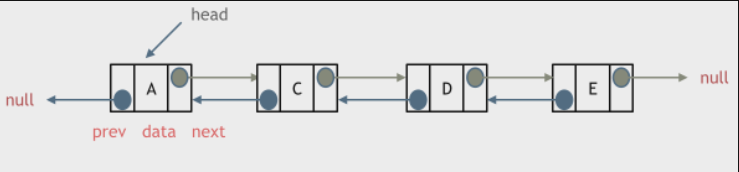    20220526212848
    20220526212848

  3. 循环链表：
    循环链表可用来解决约瑟夫环问题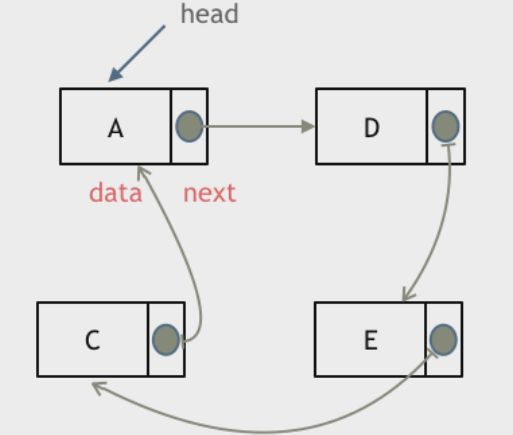

    20220526212919
    20220526212919

链表中的节点在内存中不是连续分布的 ，而是散乱分布在内存中的某地址上，分配机制取决于操作系统的内存管理。

// 单链表
struct ListNode {
    int val;  // 节点上存储的元素
    ListNode *next;  // 指向下一个节点的指针
    // ListNode *prev;  //指向前一个元素 双链表，记得构造函数初始化
    ListNode(int x) : val(x), next(NULL) {}  // 节点的构造函数
};

性能分析

插入/删除 查询 适用场景
数组 O(n) O(1) 数据量固定，频繁查询，较少增删
链表 O(1) O(n) 数据量不固定，频繁增删，较少查询

单链表的删除操作一般有两类：

  1. 设置虚拟头，将头节点当作普通节点处理，最后在删除虚拟头
  2. 头节点和其他节点分开处理

Pyhton、Java等语言可以自动释放内存，C++记得要手动释放内存节约空间。

C++示例

class MyLinkedList {
public:
    // 定义链表节点结构体
    struct LinkedNode {
        int val;
        LinkedNode* next;
        LinkedNode(int val):val(val), next(nullptr){}
    };

    // 初始化链表
    MyLinkedList() {
        _dummyHead = new LinkedNode(0); // 这里定义的头结点 是一个虚拟头结点，而不是真正的链表头结点
        _size = 0;
    }

    // 获取到第index个节点数值，如果index是非法数值直接返回-1， 注意index是从0开始的，第0个节点就是头结点
    int get(int index) {
        if (index > (_size - 1) || index < 0) {
            return -1;
        }
        LinkedNode* cur = _dummyHead->next;
        while(index--){ // 如果--index 就会陷入死循环
            cur = cur->next;
        }
        return cur->val;
    }

    // 在链表最前面插入一个节点，插入完成后，新插入的节点为链表的新的头结点
    void addAtHead(int val) {
        LinkedNode* newNode = new LinkedNode(val);
        newNode->next = _dummyHead->next;
        _dummyHead->next = newNode;
        _size++;
    }

    // 在链表最后面添加一个节点
    void addAtTail(int val) {
        LinkedNode* newNode = new LinkedNode(val);
        LinkedNode* cur = _dummyHead;
        while(cur->next != nullptr){
            cur = cur->next;
        }
        cur->next = newNode;
        _size++;
    }

    // 在第index个节点之前插入一个新节点，例如index为0，那么新插入的节点为链表的新头节点。
    // 如果index 等于链表的长度，则说明是新插入的节点为链表的尾结点
    // 如果index大于链表的长度，则返回空
    void addAtIndex(int index, int val) {
        if (index > _size) {
            return;
        }
        LinkedNode* newNode = new LinkedNode(val);
        LinkedNode* cur = _dummyHead;
        while(index--) {
            cur = cur->next;
        }
        newNode->next = cur->next;
        cur->next = newNode;
        _size++;
    }

    // 删除第index个节点，如果index 大于等于链表的长度，直接return，注意index是从0开始的
    void deleteAtIndex(int index) {
        if (index >= _size || index < 0) {
            return;
        }
        LinkedNode* cur = _dummyHead;
        while(index--) {
            cur = cur ->next;
        }
        LinkedNode* tmp = cur->next;
        cur->next = cur->next->next;
        delete tmp;
        _size--;
    }

    // 打印链表
    void printLinkedList() {
        LinkedNode* cur = _dummyHead;
        while (cur->next != nullptr) {
            cout << cur->next->val << " ";
            cur = cur->next;
        }
        cout << endl;
    }
private:
    int _size;
    LinkedNode* _dummyHead;

};

关于环形链表和入口问题

链表是否存在环可以用双指针快速判定，fast每次移动两个节点，slow一个节点，如果相遇（即fast == slow），则必定存在环

环的入口可以这样求：在相遇位置设置tmp1，在链表头结点处设置tmp2，每次走一个节点，相遇位置即为环入口节点

理论比较简单，详细可参见链表：环找到了，那入口呢？,dalao写的非常详细