贪心的 本质是选择每一阶段的局部最优,从而达到全局最优
本篇为个人笔记,内容或有错误。
图片部分源于代码随想录,侵删。
思路
贪心的题目没有固定套路,但都遵循着一个思想:局部最优从而达到全局最优
简单的问题直接遵循这个思想解决即可,稍微麻烦一点的可能会涉及到两个维度最优,且两个维度相互有联系,相互牵制,就比如下面这道题,首先要根据题目确定一个合适的维度保持最优,然后调整另一个维度。
eg
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [$h_i$, $k_i$] 表示第 i 个人的身高为 $h_i$ ,前面 正好 有 $k_i$ 个身高大于或等于 $h_i$ 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
示例 1:
- 输入:people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
- 输出:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
- 解释:
- 编号为 0 的人身高为 5 ,没有身高更高或者相同的人排在他前面。
- 编号为 1 的人身高为 7 ,没有身高更高或者相同的人排在他前面。
- 编号为 2 的人身高为 5 ,有 2 个身高更高或者相同的人排在他前面,即编号为 0 和 1 的人。
- 编号为 3 的人身高为 6 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
- 编号为 4 的人身高为 4 ,有 4 个身高更高或者相同的人排在他前面,即编号为 0、1、2、3 的人。
- 编号为 5 的人身高为 7 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
- 因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。
示例 2:
- 输入:people = [[6,0],[5,0],[4,0],[3,2],[2,2],[1,4]]
- 输出:[[4,0],[5,0],[2,2],[3,2],[1,4],[6,0]]
提示:
- 1 <= people.length <= 2000
- 0 <= $h_i$ <= 10^6
- 0 <= $k_i$ < people.length
题目数据确保队列可以被重建
本题有两个维度,h和k,看到这种题目一定要想如何确定一个维度,然后在按照另一个维度重新排列。
如果两个维度一起考虑一定会顾此失彼。
对于本题究竟先按h排序呢,还先按照k排序呢?
如果按照k来从小到大排序,排完之后,会发现k的排列并不符合条件,身高也不符合条件,两个维度哪一个都没确定下来。
那么按照身高h来排序呢,身高一定是从大到小排(身高相同的话则k小的站前面),让高个子在前面。
此时我们可以确定一个维度了,就是身高,前面的节点一定都比本节点高!
那么只需要按照k为下标重新插入队列即可。
局部最优:优先按身高高的people的k来插入。插入操作过后的people满足队列属性
全局最优:最后都做完插入操作,整个队列满足题目队列属性
本题整个插入过程如下:
排序完的people:
[[7,0], [7,1], [6,1], [5,0], [5,2],[4,4]]
插入的过程:
- 插入[7,0]:[[7,0]]
- 插入[7,1]:[[7,0],[7,1]]
- 插入[6,1]:[[7,0],[6,1],[7,1]]
- 插入[5,0]:[[5,0],[7,0],[6,1],[7,1]]
- 插入[5,2]:[[5,0],[7,0],[5,2],[6,1],[7,1]]
- 插入[4,4]:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
此时就按照题目的要求完成了重新排列。
class Solution {
public:
static bool cmp (vector<int>& a, vector<int>& b) {
if (a[0] == b[0]) return a[1] < b[1];
return a[0] > b[0];
}
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
sort(people.begin(), people.end(), cmp);
vector<vector<int>> res;
for (int i = 0; i < people.size(); i++) {
res.insert(res.begin() + people[i][1], people[i]);
}
return res;
}
};
- 时间复杂度:$O(nlog n + n^2)$
- 空间复杂度:O(n)
2022/8/6
有一类区间最优问题非常适合贪心,比如下面几题:
这类区间问题有一个套路就是可以先对区间排序,至于是根据左边界排序还是右边界没有太大影响,个人习惯左边界排序,之后通过控制右边界即可轻松解决问题,上文也提到不要一起考虑,不然容易顾此失彼。
根据左边界排序之后,所有的区间左边界必定是递增的(当然不是严格递增,存在相等的情况),而右边界无非三种情况,相对于我们选定的右边界来说,大于,小于,等于,此时只需要根据题目要求针对三种情况处理即可,这样就可以保证处理位置之前的区间都是最优的,也就是局部最优,待遍历到末尾之后,前面都是局部最优解,最终也就是全局最优,总之还是贪心没有固定套路,最多只能是几类问题有相似之处而已,从问题中找到局部最优解,然后扩展到全局即可。
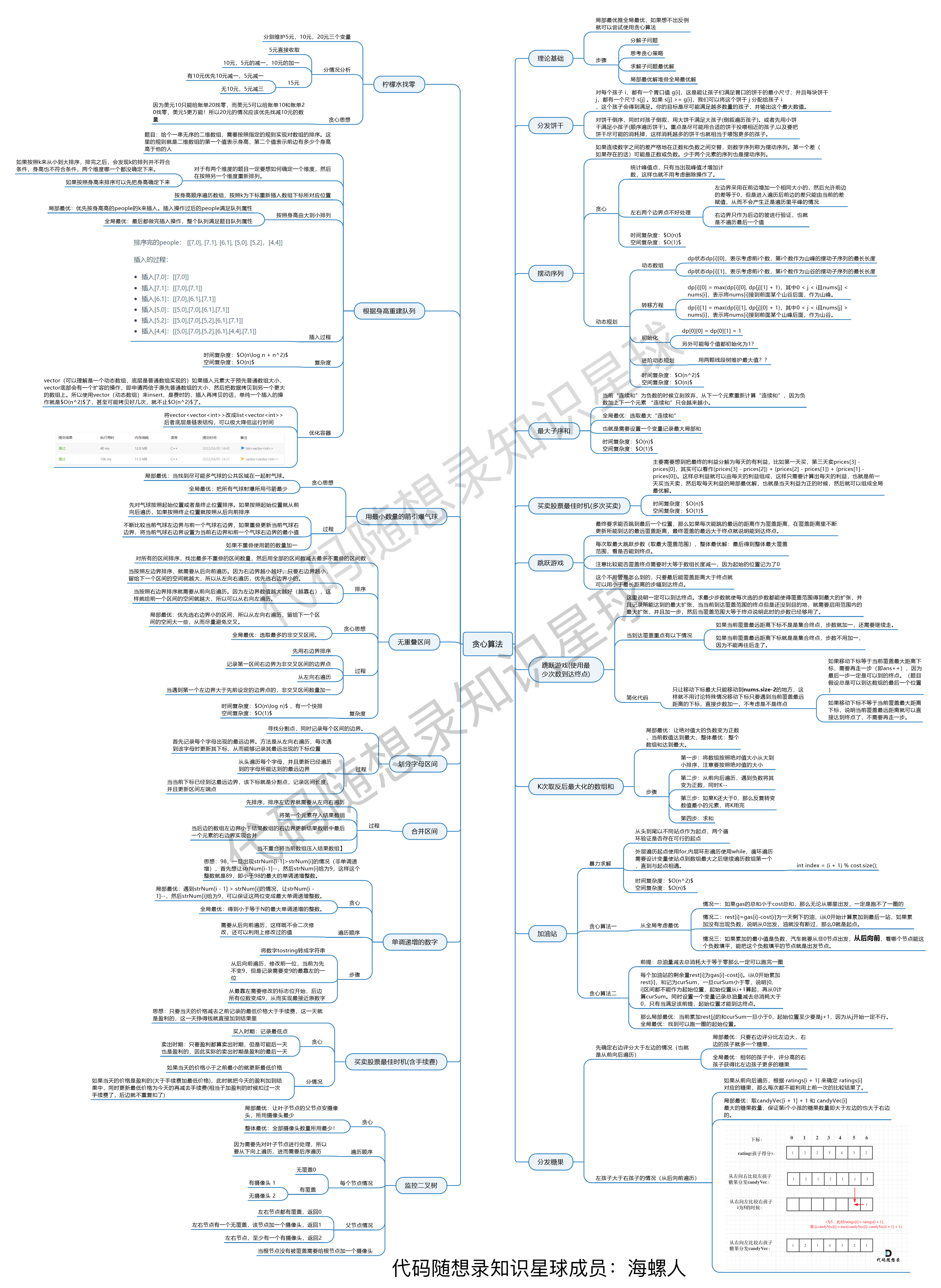
最后附上贪心的知识图(图源知识星球:海螺人):