动规
本篇为个人笔记,内容或有错误。
图片部分源于代码随想录,侵删。
动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。
所以动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的
动规的五部曲
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
如果代码写出来了,一直AC不了,灵魂三问:
- 这道题目我举例推导状态转移公式了么?
- 我打印dp数组的日志了么?
- 打印出来了dp数组和我想的一样么?
首先要明白dp数组的含义是什么,下表代表什么,确定了这个之后按照套路走就行,手动推导dp数组本质上也是一种检验的过程,当打印出结果符合预期手动推导结果时,基本就没太大问题
2022.8.9
动态规划的习题我认为最重要的就是要确定dp数组的定义,下标代表什么,该如何初始化,举个例子:
给定一个正整数 n,将其拆分为至少两个正整数的和,并使这些整数的乘积最大化。 返回你可以获得的最大乘积。
示例 1:
- 输入: 2
- 输出: 1
- 解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
说明: 你可以假设 n 不小于 2 且不大于 58。
这道题在我的做法中dp数组表示的是i这个数字的最大拆分乘积,初始化dp[2] = 1,这是易知的,而在一些题解中就把dp[0]和dp[1]也进行了初始化,这么做当然也可以AC,但是dp数组的意义已经模糊了,暂不谈题目限制`$$2 \le n \ge 58$$,就按照题目说明,0和1就不能拆分为两个正整数的和,更不用谈乘积,虽然这么初始化问题也不大,但是我感觉要透过题去理解,要明白dp数组的含义,下标表示了什么更为重要,下面是本题C++代码:
class Solution {
public:
int integerBreak(int n) {
vector<int> dp(n + 1);
dp[2] = 1;
for (int i = 3; i <= n ; i++) {
for (int j = 1; j < i - 1; j++) {
dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
}
}
return dp[n];
}
};
- 时间复杂度:O(n^2)
- 空间复杂度:O(n)
背包问题2022.08.10
转载自代码随想录,侵删
建议按照如下顺序观看:
背包理论基础01背包1
背包理论基础01背包2
背包基础理论完全背包
背包基础理论多重背包
01背包和完全背包2022.08.13
背包问题大概描述是:有一个承重m的背包,旁边有一堆物品共n个,每个物品重量不一,价值不易,weight[i]和value[i]分别代表第i个物品的重量和价值,求背包最多能装下物品的价值
01背包是说每个物品只有一个,怎么装价值最大
完全背包是说每种物品有无限多个,怎么装价值最大,比如一辆卡车去进货,每种货占的空间不同,价值也不同,但是每种货数量是不限制的,怎么装,一卡车货价值最大
01背包-二维-先物品后背包
采用二维数组遍历必然要考虑遍历顺序,是先遍历背包,还是先遍历物品,不妨设先遍历物品,那么循环内层遍历的就是背包了
当对于num[i],无非两种情况:
- 背包可以装的下,继续装那么价值就是
dp[i - 1][j - weight[i]] + value[i],表示未装num[i]物品前,背包最大容量必然是j - weight[i](因为还要装第i件物品,所以预留出weight[i]的空间,剩下的空间可以装的最大值就是dp[i - 1][j - weight[i]]) - 装不下,背包里面物品价值还是不变,就是
dp[i - 1][j]
那么二者取最大值,就是i件物品容量为j的背包可以装的物品最大价值,依次递推即可
for (int i = 0; i < num[i]; i++) {
for (int j = weight[i]; j <= target; j++) { //j从weight[i]开始,是因为小于weight[i]的背包根本装不下第i件物品,所以一定都是dp[i - 1][j]
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
01背包-二维-先背包后物品
转变一下遍历顺序二维时是完全可以的,观察上述递归公式可以发现,dp[i][j]完全是由上一行的值和weight数组和value数组决定的,而后面两个是已知的,所以不管按照什么顺序遍历,dp[i][j]仅由其左上位置数值决定,所以遍历顺序怎么样都可以,下面给出先遍历背包,后遍历物品的代码:
for (int j = 0; j <= target; j++) {
for (int i = 1; i < nums.size(); i++) {
if (j < weight[i]) dp[i][j] = dp[i - 1][j]; //装不下
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); //装得下
}
}
01背包-一维
前面也已经说明过了,dp[i][j]只依赖上一行的数值,所以我们可以将dp数组降为一维,节约空间,但是要注意,二维的时候我们依赖的是上一行(i - 1行)的值,降为一维后,当不做任何变化时,当前数值就是上一行数值,但是如果j还是从前往后遍历,那么当为j时,从0 ~ (j - 1)的数值已经变为新值了,不再是上一行的值,所以不能从前往后遍历,而当我们从后往前遍历则是可以的,原因也很简单,前面说过,dp[i][j]只依赖左上方的值,当降为一维数组之后,就是只依赖左方的值,而我们从后往前遍历,左方的值一直都未变化,当然是可以的,代码如下:
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
顺序在这里也很重要,一定要是先物品后背包容量,反之则不行
观察二维时候的递推公式
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
dp[i][j]依赖的是上一行,不是上一列,是j - weight[i]列,所以滚动数组完全不可行
完全背包
完全背包相比01背包就是物品可以用无数次,仅仅在01背包的基础上略微修改即可,从前往后遍历即可
上文知道,01背包从后往前遍历是为了保证每个物品仅仅使用一次,而完全背包可以用无数次,从前往后即可,代码如下:
// 先遍历物品,再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
// 先遍历背包,再遍历物品
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
for(int i = 0; i < weight.size(); i++) { // 遍历物品
if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
cout << endl;
}
至于遍历顺序,则同01背包
关于排列和组合
完全背包往往会涉及到排列和组合的问题
就比如这个组合总数Ⅳ,求数字总和为target
这道题目要求数字顺序不一样也是一种组合,其本质上就是排列问题,那么使用循环遍历时就需要注意遍历顺序了
先物品后背包肯定是行不通的,因为物品只能按顺序出现,比如说{1, 3},不可能出现{3,1},因为物品是在外侧循环,只能按照数组顺序出现,所以说不能使用先物品后背包的方式,而要用先背包后物品才可以
一句话总结就是先物品后背包是组合 , 先背包后物品是排列
多重背包
多重背包其实跟01背包如出一辙,只是原本数量为1的物品现在数量不再一定为1了,而是由一个数量数组nums记录每件物品的数量有多少,针对多重背包,有以下两种解决方法:
- 把多重背包拆分为01背包,把同一种物品拆分为一个一个的,问题就简化为了01背包,按照01背包的解决方法即可
- 在双重遍历的时候内嵌一个for循环,遍历这个物品对应的数量即可,本质上还是把同一个物品拆分为了一个一个的
背包总结
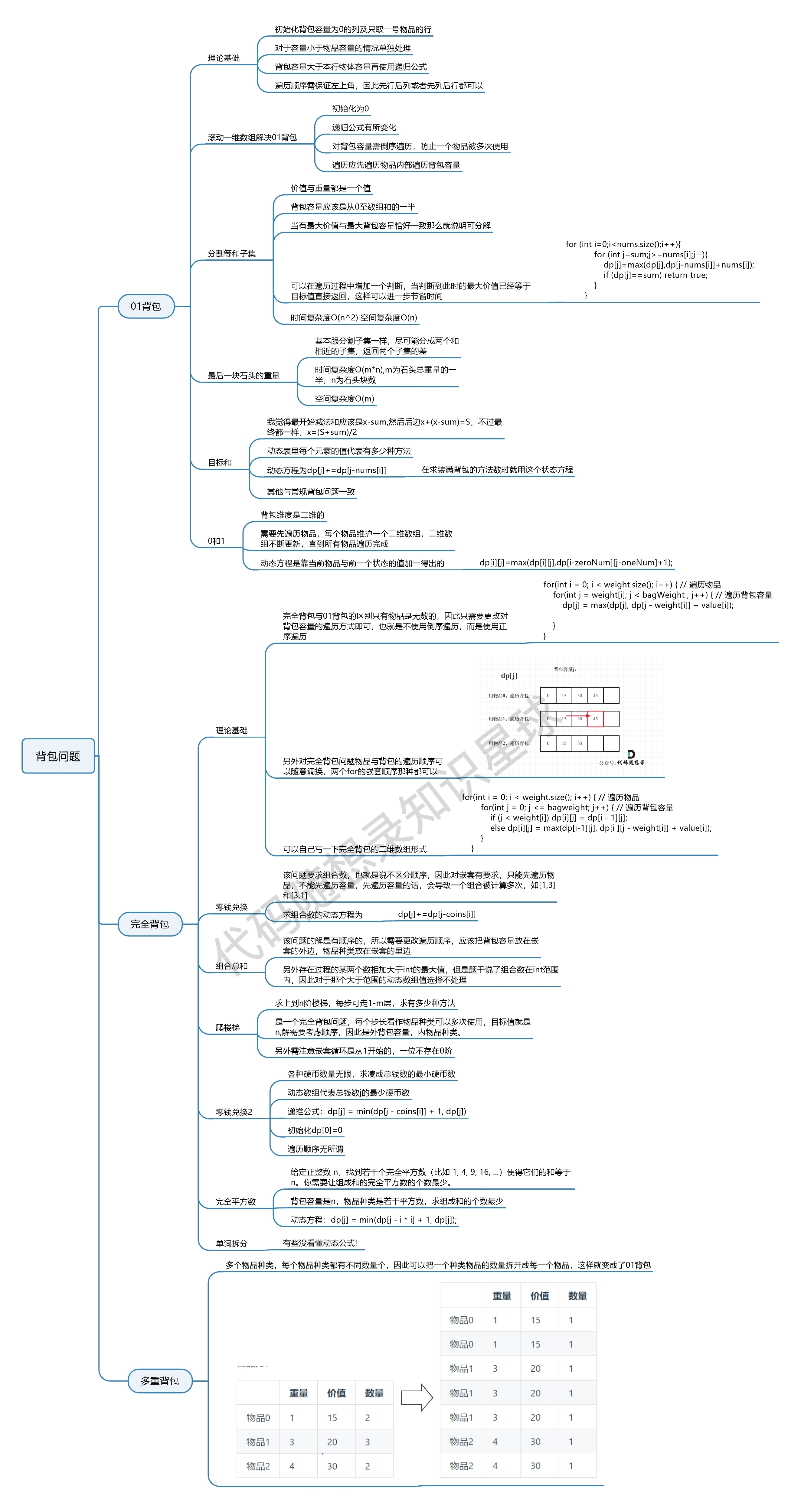
图源代码随想录知识星球 (opens new window)成员:海螺人